Die Kohlrausch'sche Walzenbrücke
ist der Abgleichwiderstand für eine Wheatston'sche Brückenschaltung.
Nein, natürlich nicht, denn das kurze Fachchinesisch wird durch das längere Kryptogramm nicht erläutert.
Aber ... willst du es wirklich wissen?
Es geht um ein wissenschaftliches Messverfahren- zur möglichst genauen Bestimmung von Widerstandswerten oder
- für die haargenaue Messung von minimalen Veränderungen des Widerstands durch Temperatur, Magnetfeld, ...
Wenn du es wirklich wissen willst, es funktioniert so:
Hinweis nebenbei:
Der Physiker braucht das Wort "Widerstand" in doppelter Bedeutung.Er meint zum einen das Gerät selbst,
also die Glühbirne ist ein Widerstand, die Waschmaschine, das Bauteil, die LED, usw. alles sind Widerstände.
Er meint zum anderen die Eigenschaft des Gerätes, wie es die Stromstärke beeinflusst:
Die 60-Watt-Glühbirne hat einen Widerstand von 900 Ohm, die 40-Watt-Glühbirne hat einen Widerstand von 1,3 kOhm, usw.
- Der Unterschied bedeutet,
dass durch die 60iger mehr Strom fließt (weil der Widerstand kleiner ist) und sie
heller brennt.
Und oft benutzt er beide Bedeutungen gleichzeitig.

Widerstands-Messung, einfach:
Widerstands-Skala auf einem Vielfach-Messinstrument.
Ein Widerstand (Gerät) wird an eine feste Spannung (ist im Messinstrument vorhanden, Batterie) angeschlossen und der Strom wird gemessen. Das Messinstrument zeigt den Strom (obere Skala) und gleichzeitig auf der zugeordneten unteren Skala den Widerstand (Eigenschaft) an.Die Genauigkeit ist besser als 10% und reicht für Techniker und Bastler aus.
Widerstands-Messung, super genau:
In einer etwas aufwändigeren Schaltung (Wheatston'sche Brücke) wird derunbekannte Widerstand Rx (Gerät, hat den unbekannten Widerstand Rx (Eigenschaft))
mit einem Messwiderstand Rm (Gerät, hat den bekanntem Widerstand Rm (Eigenschaft))
verglichen.
Damit Messwiderstand und Prüfling nicht genau gleich groß sein müssen, das wäre eine monatelange Probiererei, nimmt man einen Abgleichwiderstand hinzu, teilt ihn in zwei veränderlich große Teile und stellt deren Größe so ein, dass
- das Verhältnis Rx zu Rm
- gleich ist
-
dem Verhältnis der beiden Teile des Abgleichwiderstandes (Teil 1 zu Teil 2).
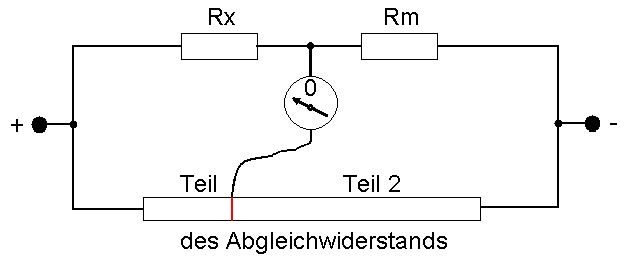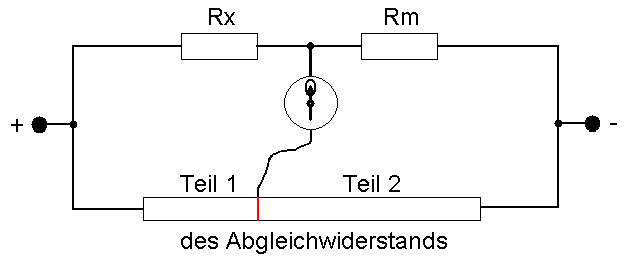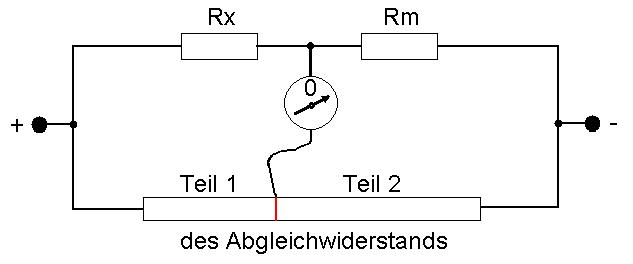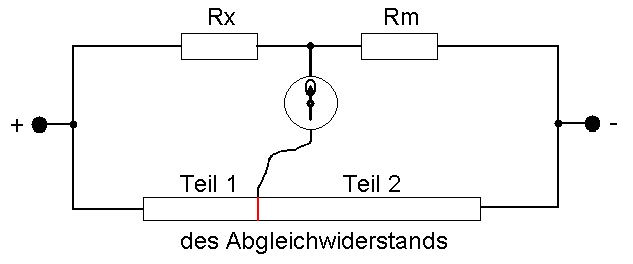
Das wird mit dem (sehr empfindlichen!) Messinstrument kontrolliert, das beim Abgleich den Wert „0" zeigt.
Der Rest ist Mathematik.
- 1. wie genau der Messwiderstand ist.
- 2. wie genau das Verhältnis der Teile des Abgleichs bestimmt werden kann.
- und es gilt:
- zu 1.: Da erreicht man eine Genauigkeit im Bereich von Hundertstel Prozent.
- zu 2.: Also ... öh ..., tut mir leid, aber da muss ich etwas weiter ausholen:
In Schulversuchen nimmt man einen Draht von 50 cm Länge mit einer Millimeterskala darunter und einem Schleifkontakt darüber und liest die Teillängen des Drahtes ab. Das geht auf einige mm genau, eine höhere Genauigkeit ist nicht erforderlich, da die Schüler das Prinzip lernen sollen und nicht supergenaue Ergebnisse vorweisen müssen.
In der Wissenschaft nimmt man einen viel längeren Draht, mehr als fünf Meter lang, und den muss man handhaben können.
Die folgende Anordnung ist nach Friedrich Kohlrausch (14.10.1848 - 17.01.1910) benannt:Der Draht wird auf eine Walze (= drehbare Trommel) gewickelt (hier 17 Windungen) und an den beiden festen Anschlüssen fixiert.
Der dritte Anschluss besteht aus Rollen, die den Draht berühren (Kontakt), von ihm geführt werden (Ortsänderung) und den Strom über eine seitliche Schiene ableiten.
Ablesung der Länge:
Jede Windung des Drahtes entspricht einem Siebzehntel der Gesamtlänge.
Die Skala am Drehknopf zeigt 360° für eine volle Umdrehung.
Die Gesamtlänge des Drahtes wird also in 17 x 360 = 6120 messbare Teile zerlegt.
Dadurch kann ein Messwert mit der beeindruckenden Genauigkeit von 0,02 Prozent bestimmt werden, und diese Genauigkeit ist der Grund und Zweck für den ganzen Aufwand.
Steht die Rolle auf der 5. Windung des Drahtes, entspricht das 5/17 der Gesamtlänge oder 5 x 360 = 1800 Teilen.
Zeigt die Skala zusätzlich genau 180°, entspricht das der Hälfte einer Einzelwindung = 180 Teile. Zusammen 1800 + 180 = 1980 Teile des Drahtes.
Die Anzeige ist also: 1980 von 6120 = 11 von 34 oder 11 zu 23. Das ist das Verhältnis, in dem der Draht in seiner Länge und damit auch als Widerstand aufgeteilt ist, damit rechnet man weiter.